Linear Control Systems Demonstration

For the October 9^th WCRS meeting, Russ Hersberger was asked to demonstrate Linear System Analysis using a piece of equipment from the linear control systems lab here at SAIT. The point was to show the group some analytical tools for building better robots. Russ enjoys explaining motors much more, and since I was experimenting with the other equipment anyway, he asked me to do the linear systems presentation so he could present an equally exciting motor analysis. This way, we had the opportunity to show much more than we expected to. What a great experience, and what a great turnout. Thank you to everyone who showed such interest in our presentations. For all those who did not have to opportunity to see it, here is an overview of what it was all about.

Linear Control Systems Analysis is all about understanding physical systems and how they interact. Ideally we should be able to model any system in terms of math, and most non-linear systems can be linearized, or simplified to make them a little easier to work with. The bottom line is that we can get a pretty good idea of how just about any physical system will work with this kind of analysis. 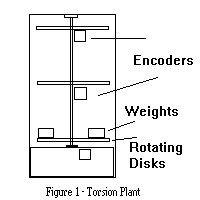The equipment we demonstrated can give us a physical representation, or test-bed for those linear equations. Specifically, I presented the Torsion Plant, which is a vertically oriented rotational system of 3 disks connected by a thin steel shaft, which acts as a rotational spring. The disks can each accept a series of weights and a high precision motor drives the center shaft. The whole assembly is connected to a computerized feedback control system with data acquisition through 3 very sensitive encoders. (See figure 1)

If you were there, you had the opportunity to ‘feel the math’ so to speak. Using the software and feedback control system, we were able to give people a hands-on sample of the effects of integration and differentiation. To relate this to the robot world, this means, "What happens when my walker’s leg presses up against an obstacle", and "why does my line-tracker fly off the track so easily". I was particularly interested to see seasoned engineers, who understand the math and physics implicitly, finally get a chance to feel the effects of an integrating force pressing back against their hands. And then say "Wow, that’s cool."

By changing a few numbers in the feedback loop in software we could show what happens to a robot’s axel when the tires lock on an obstacle. Change a few other numbers and we can show you how to build a more precise line follower though differentiation. Another change, and we are looking at a motor circuit on the verge of instability. Even though the demonstration was on a rotational mechanical system, we can use the math to simulate virtually any physical system. Input the right numbers, and you can tweak your infrared edge detector to perfection, or calculate the ideal wheelbase for your platform.

The point was to show the power of linear systems analysis and how you can benefit from the use of this technique. You don’t need $20,000 worth of hardware to do it, but it sure makes a fun presentation.

If you found this interesting and want more information about linear control analysis, I have started a short tutorial at http://www.mairs.ca/tom/papers/lcs.php where you can also find links to other references.