A Primer On Linear Control Systems Analysis
Page 2 - Matrix Manipulation:
On the previous page, we made several calculations to derive 2 state equations for our system. The figure 5 below shows those equations with the two state equations regrouped at the bottom for clarity.
Figure 5 - Regrouped state equations
A matrix is simply a way of representing a number of simultaneous equations
that refer to the same system. The matrix equation we use to describe
ALL systems is 
or State of The System
= (Physical Constants * State Variables)+(Input
Values * Inputs).
The physical constants are simply the coefficients to the x values.
The Inputs are the sources. So what we end up with is something that looks
like this:
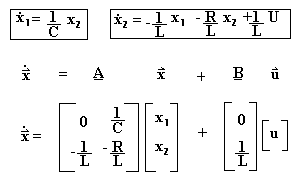
Figure 6 - The System Matrix Equation
And that's it - well, for this part anyway. This describes the physical
system in mathematical form. Now to get a value OUT of this form for analysis,
we have to look at the output matrix 
.
This part can actually be fairly simple. If you wanted to know the voltage across the capacitor, which was one of out state variables (x1), then we simply isolate that variable using a matrix of all 0's except for the variable we want. This is the C matrix. The other matrix, D, is called the feed-forward matrix and is used to apply forced sources to the output. In our case, the C matrix should be [1 0] to isolate x1 and the D matrix should be [0] because there are no feed forward sources (see figure 7 below).
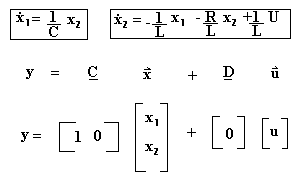
Figure
7 - The Output Matrix Equation