A Primer On Linear Control Systems Analysis

Page 3- A little Philosophy...

Remember when I mentioned that everything could be related though energy? Way back on the first page, I mentioned that ALL things could be related through their energy equations. Then, on the second page we took 3 different components and put them into the same equation to get a picture of the system's physical state. In the last example it was all electronics, but a real system could be a combination of electrical, mechanical, thermal, fluid, and other seemingly dissimilar elements. I know you are not going to believe me when I tell you they can all go into the same matrix, so let me show you how.

All things in the universe can be described in terms of energy. For a simple example, think of a book sliding across a table. The book has mass, and there is friction between it and the table. There is also the force you apply to move the book to make it move. Well look at this....

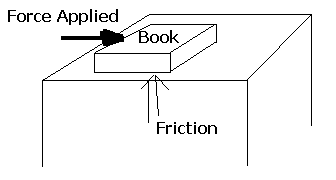
Figure 8 - Energy equations

The kinetic energy in the moving book is defined as so we can use as one of the physical variables. In fact, there is only the one physical variable in this system. The defining relationships in this system are:

Figure 9 - Mechanical Defining relations

And Newton's 3rd law says Fin=FM + FB so Fin = MDv + Bv, and if the velocity ( the physical variable) is selected as x1, then the equation unfolds like this:

Figure 9 - Mass equation

And the Matrix looks like this:

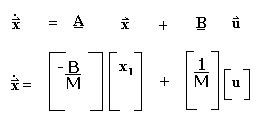
Figure 10 - Mass Matrix

This is a very simple example, and really did not require a matrix, but I did it to show the process. This matrix equation is essentially an energy snapshot of the system you are working on. In a linear, time invariant system, this equation will not change. If there is a change in the input, or a force is added to resist the book from the other side, then you simply add it to the matrix in the 'source' matrix [B]. This process can be continued on through much larger, much more complicated systems.

Figure 11 is a table of some of the Energy equations that Control Systems Engineers work with. Take notice of the pattern in the equations. The physical variables we use in our calculations are the ones that are squared in the energy equations. Those are voltage, current, velocity, distance, angular velocity, and temperature. This is not a complete list , but it should give you the idea of what to look for when building the equations you need.

Figure 11 - Energy Equations

But this isn't the only way we can deal with this system. We can also look at it as a whole in the Laplace domain.

Next... Entering the Laplace Domain.